Otro de los aspectos que permite hacer la inferencia es determinar si existe o no asociación entre diferentes variables, es decir, de unas hipótesis cuya validez debemos confirmar o rechazar.
Introducción
Para llevar a cabo esta comprobación aplicamos unas pruebas estadísticas o tests, que permiten contrastar la veracidad o falsedad de las hipótesis enunciadas desde el punto de vista estadístico, si no recuerdas este tema, te invitamos a que leas nuestro pasado Post Este tipo de pruebas se clasifican en pruebas paramétricas y pruebas no paramétricas.
En este nuevo post hablaremos de los test requeridos para considerar si nuestros datos se pueden manejar bajo las pruebas paramétricas o las no paramétricas, como supuestos de normalidad y homocedasticidad. Cabe recordar que las pruebas paramétricas exigen ciertos requisitos previos para su aplicación, donde su incumplimiento conlleva la necesidad de recurrir a pruebas estadísticas no paramétricas.
Variable de estudio: tiene que ser numérica. Esto es, la variable dependiente debe estar medida en una escala que sea, por lo menos, de intervalo.
Normalidad: El análisis y observaciones que se obtienen de las muestras deben considerarse normales.
Homocedasticidad: Las varianzas de la variable dependiente en los grupos que se comparan deben ser aproximadamente iguales, es decir, que sean homogéneas,
Errores: Los errores que se presenten deben de ser independientes. Esto solo sucede cuando los sujetos son asignados de forma aleatoria y se distribuyen de forma normal dentro del grupo.
n muestreal: La n es el tamaño de la población. En este caso, el tamaño de la población de la muestra no puede ser inferior a 30, y será mejor cuanto más se acerque a la n de toda la población.
!Bien!
Entonces empecemos a aprender a como calcular cada uno de los requisitos para determinar si podemos hacer un estudio paramétrico o no

Normalidad
La lógica de la prueba se basa en las desviaciones que presentan las estadísticas de orden de la muestra respecto a los valores esperados de los estadísticos de orden de la normal estándar.
Para estudiar si una muestra aleatoria proviene de una población con distribución normal se disponen de tres herramientas que se listan a continuación.
- Histograma y/o densidad.
- Gráfico de cuantiles teóricos (QQplot).
- Pruebas de hipótesis.
Al evaluar visualmente la simetría de la distribución de los datos a partir de un gráfico de histograma y/o densidad, si observamos que este no cumple la simetría (sesgo a uno de los lados) o si se observa una distribución con más de una moda, eso sería indicio de que la muestra no proviene de una población normal. Por otra parte, si se observa simetría en los datos, esto NO garantiza que la muestra aleatoria proviene de una población normal y se hace necesario recurrir a otras herramientas específicas para estudiar normalidad como lo son los gráficos QQplot y pruebas de hipótesis.

A continuación profundizaremos un poco sobre el uso de cada de las tres herramientas anteriormente nombradas para estudiar la normalidad.
Histograma y/o gráfico de densidad
Consiste en representar los datos mediante un histograma (Fig. 1) y/o gráfico de densidad (Fig. 2), superponer la curva de una distribución normal con la misma media y desviación estándar que muestran los datos.
Para realizar este ejemplo vamos a utilizar la base de datos
## Cargamos el paquete ggplot2
library(ggplot2)
## Calculamos la media y desviación estándar para la longitud del sépalo
distmean <- mean(iris$Sepal.Length)
distsd <- sd(iris$Sepal.Length)
## Y graficamos
ggplot(data = iris, aes(x = Sepal.Length)) +
geom_histogram(aes(y = ..density.., fill = ..count.., color=..count..),
alpha = 0.7, binwidth = 0.2) +
stat_function(fun = dnorm, colour = "black", size=2,
args = list(mean = distmean, sd = distsd))+
xlab("Distancia") +
ylab("Densidad")+
theme(axis.title.y = element_text(size = 18),
axis.title.x = element_text(size = 18),
axis.text.y = element_text(size = 16),
axis.text.x = element_text(size = 14))+
theme(panel.border = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.line = element_line(colour = "black", size = 1),
panel.background = element_blank())+
theme(legend.key = element_blank())+
labs(colour = "Cantidad", fill = "Cantidad")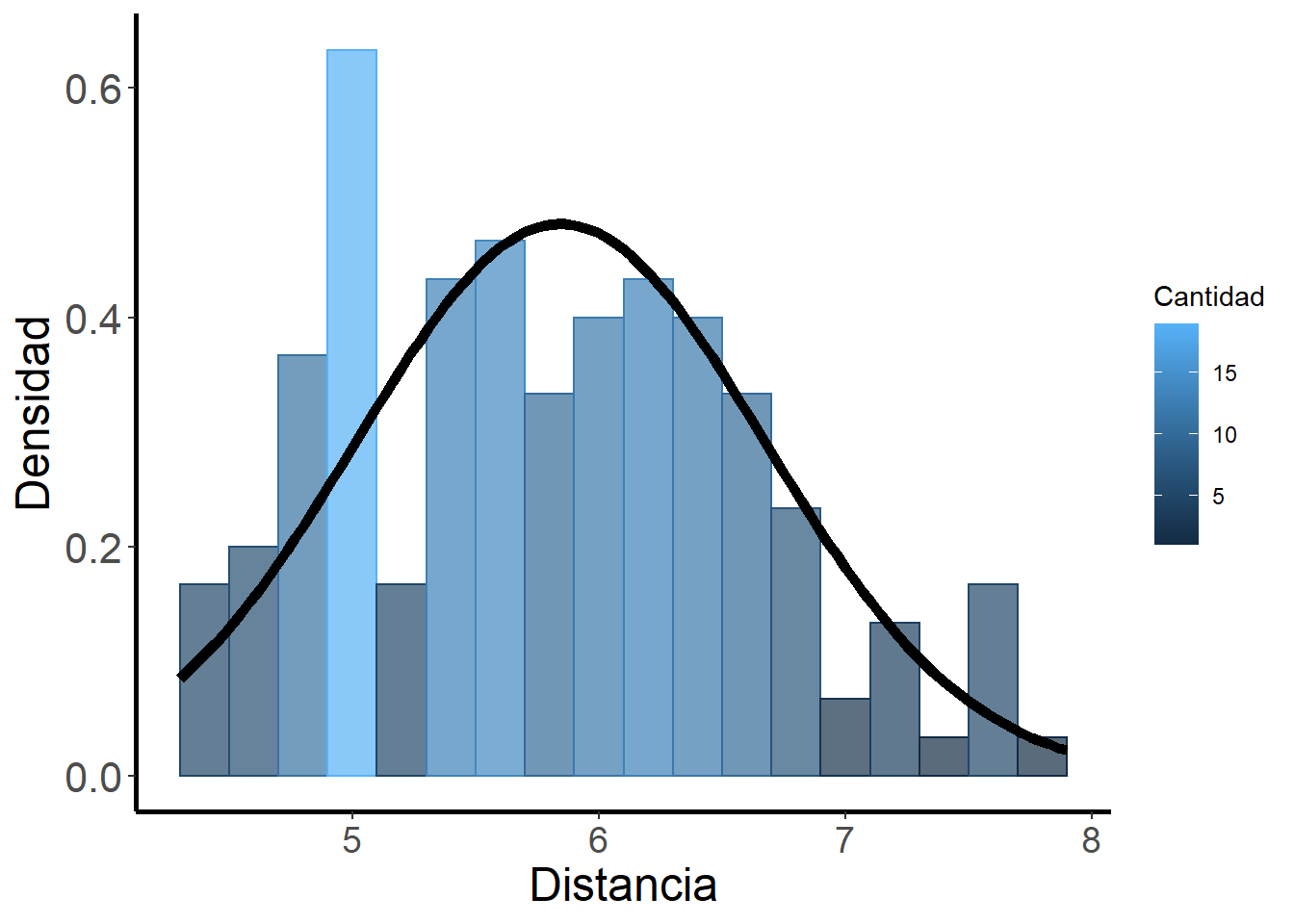 Fig. 1. Histograma y Curva normal teórica de la longitud del sépalo de las flores del género Iris
Fig. 1. Histograma y Curva normal teórica de la longitud del sépalo de las flores del género Iris
- Gráfica de densidad
plot(density(iris$Sepal.Length), main = 'Density Plot of Sepal Length', xlab = ' Sepal Length')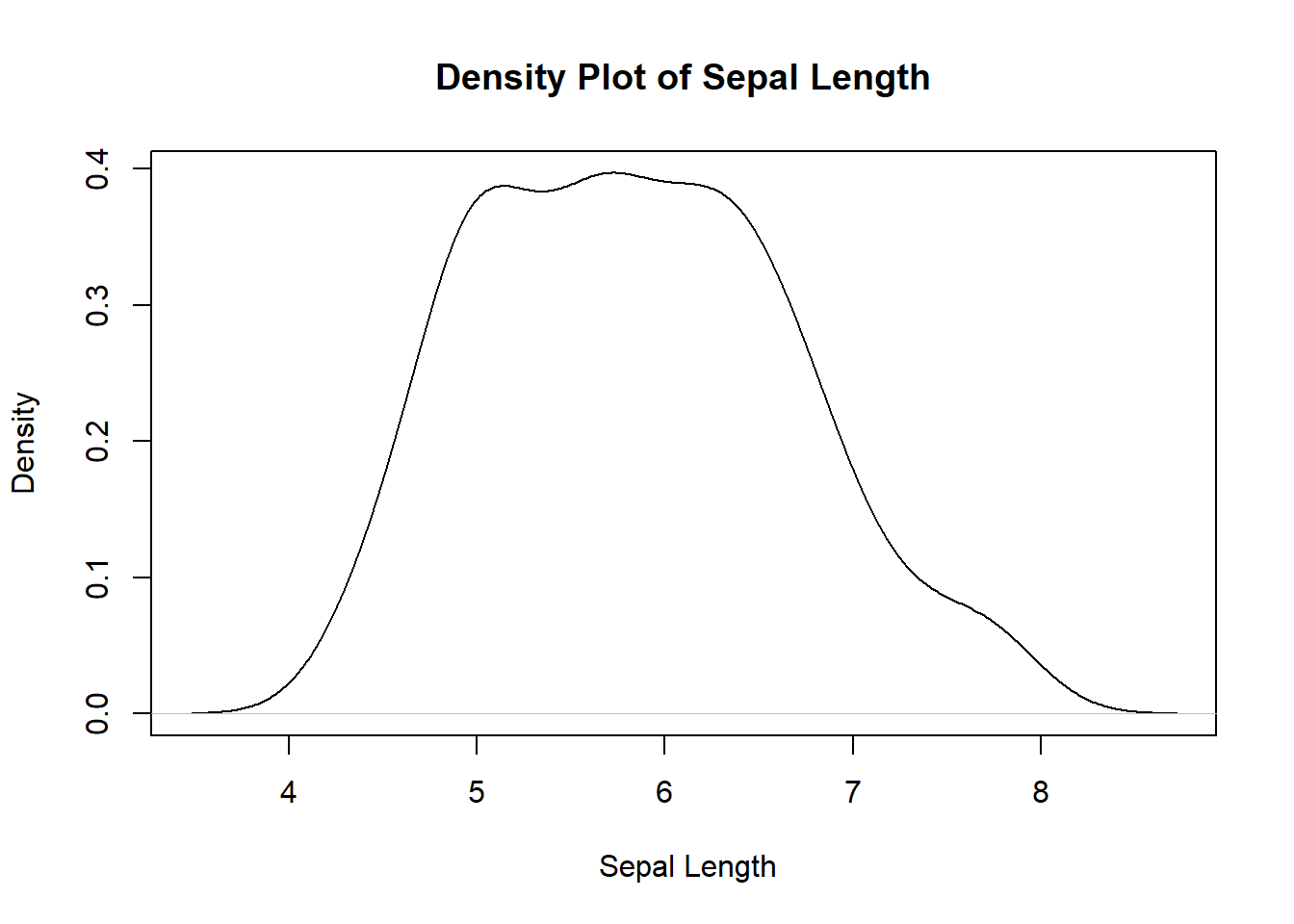
Fig. 2. Histograma y Curva normal teórica de la longitud del sépalo de las flores del género Iris
Como muestran la gráficas, no queda claro el cumplimiento de la normalidad. Visualmente, la variable sepal lenght NO parece distribuida normalmente. En el gráfico de densidad se puede apreciar que tiene una parte superior plana con sesgo positivo. Esto es bastante común, por lo que el uso de todas las herramientas es fundamental para no caer en malas desiciones.
Gráfico de cuantiles teóricos (qqplot)
Consiste en comparar los cuantiles de la distribución observada con los cuantiles teóricos de una distribución normal con la misma media y desviación estándar que los datos. Cuanto más se aproximen los datos a una normal, más alineados están los puntos entorno a la recta. Este gráfico (Fig. 3) lo realizamos con la función
qqnorm(iris$Sepal.Length, pch = 1, frame = FALSE,
main = "Gráfico Q-Q",
xlab = "Cuantiles teóricos",
ylab = "Quantiles de la muestra")
qqline(iris$Sepal.Length, col = "steelblue", lwd = 2)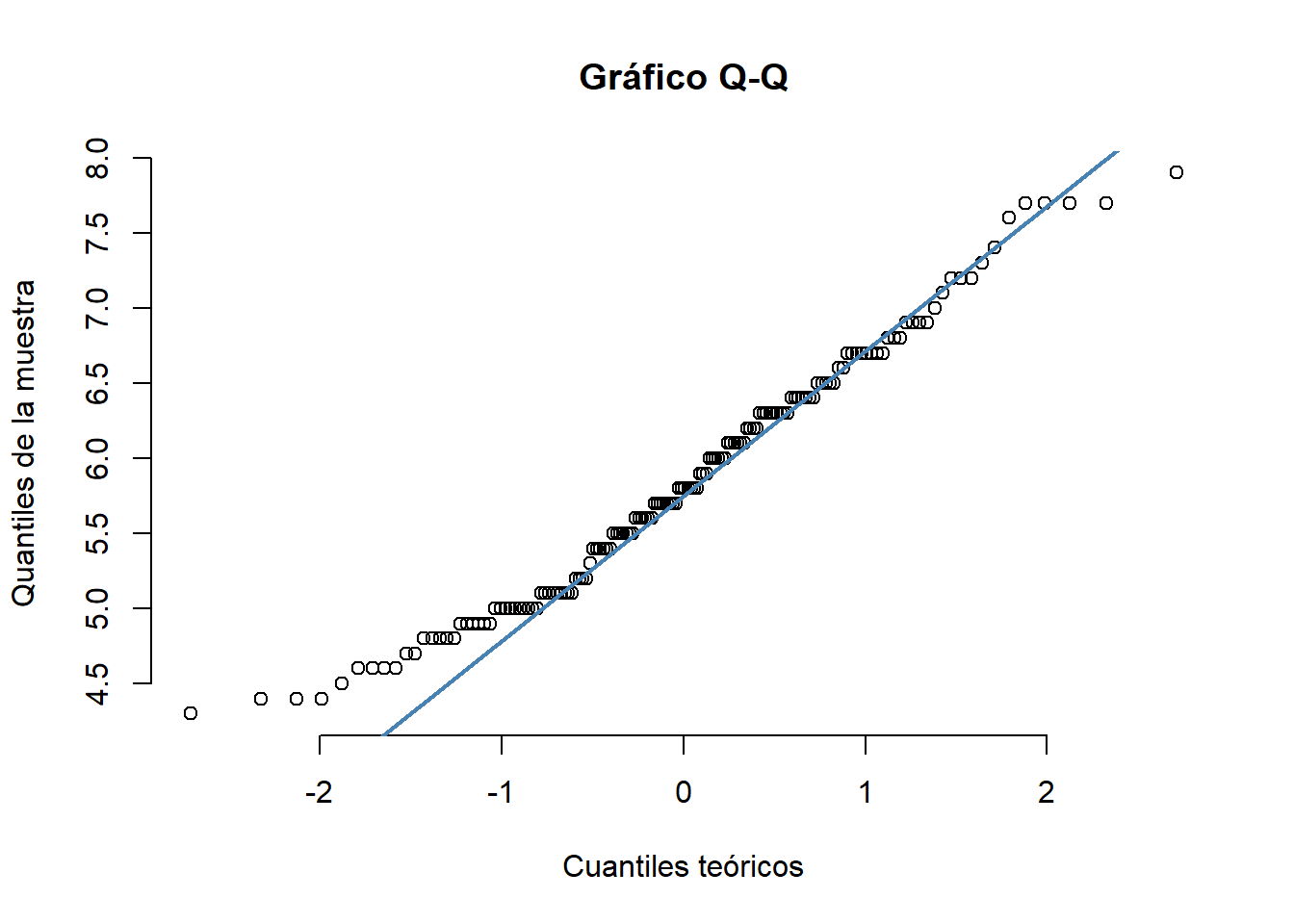
Fig. 3. Gráfico de cuantiles teóricos con el la función qqnorm de la longitud del sépalo de la base de datos iris
Otra forma de ver el comportamiento de nuestros datos es con el paquete
## El paquete "car", tiene como dependencia "carData"
library(car)
qqPlot(iris$Sepal.Length, pch = 16, col = c("black"),
col.lines = "blue", cex = 1,
main = "Gráfica Q-Q", id = F )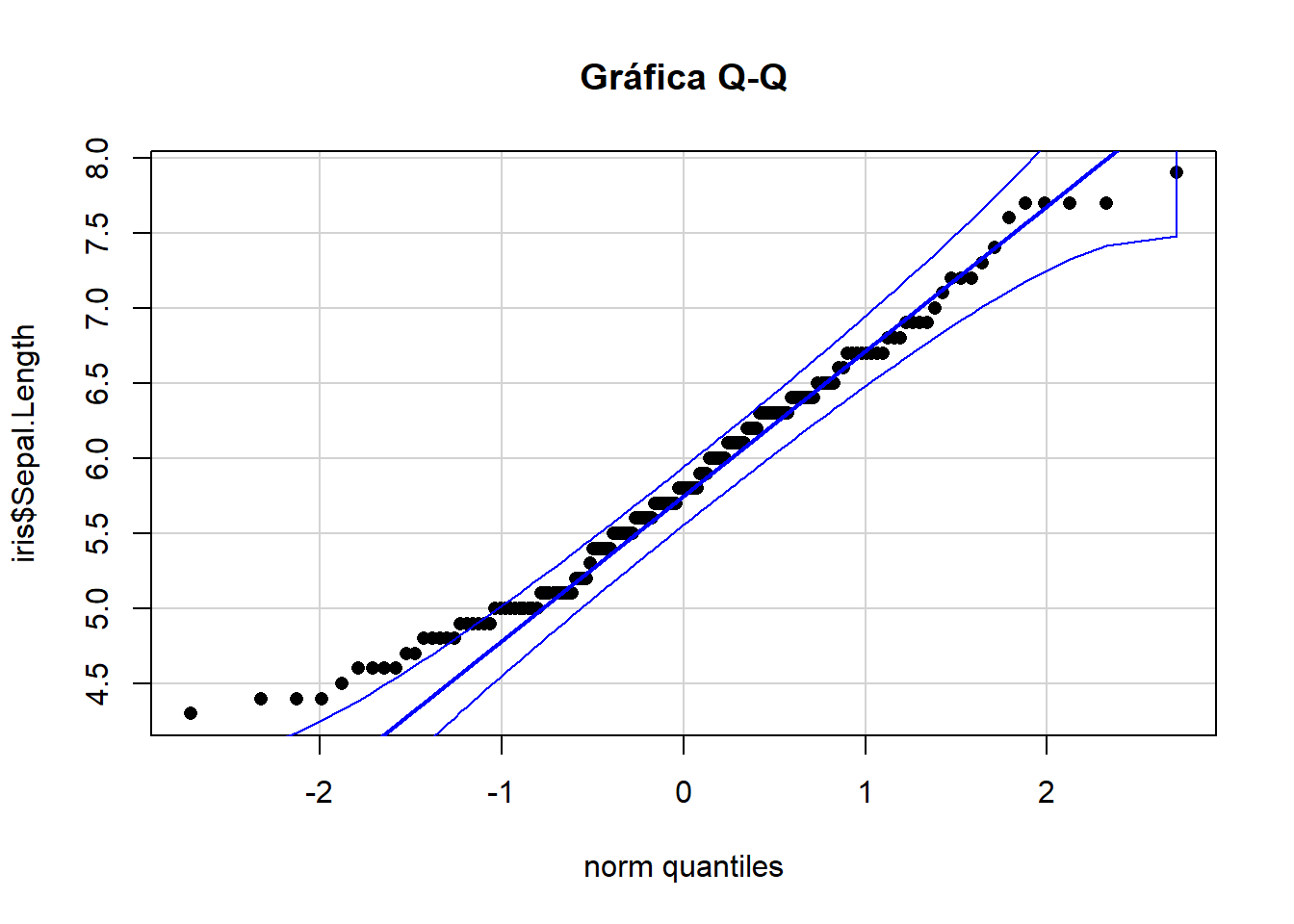
Fig. 4. Gráfico de cuantiles teóricos con el la función qqPlot de la longitud del sépalo de la base de datos iris
De acuerdo al comportamiento en el gráfico Q-Q, podemos indagar que nuestros datos si parecen cierta distribución normal, observemos que los puntos parecen caer sobre una línea recta, sin embargo, como bien habíamos dicho anteriormente, es mejor realizar todos los pasos para no cometer algún error de apreciación.
- Pruebas de hipótesis
Para poder asumir y contrastar los valores de las diferentes pruebas de hipótesis que veremos a continuación, es necesario tener bajo consideración el Test de hipótesis, el cual formularemos con un nivel de significancia de
Hipótesis nula (H0): Los datos siguen una distribución normal
Hipótesis alternativa (Ha): Los datos no siguen una distribución normalBajo la siguiente decisión: si el valor p es menor al valor α (p < α), la prueba estadística es significativa, no existiría normalidad en los datos.
Los paquetes que utilizaremos para realizar las diferentes pruebas son
Para realizar los test de Normalidad de los datos, existen varias pruebas que podremos trabajar. Estas difieren entre ellas por lo métodos utilizados y/o cantidad de datos, así que siempre es mejor profundizar en los métodos que estamos utilizando para tener pleno conocimiento de lo que andamos haciendo.
A continuación veremos algunas de ellas

- Prueba de Anderson-Darling
Es una prueba no paramétrica sobre los datos de una muestra que provienen de una distribución específica. Principalmente se basa en la distancia de la distribución hipotética F, y la función de la distribución empírica Fn, donde n es el número de elementos en la muestra.
El número de muestra debe de ser mayor a 7 y permite missing values.
## Paquete "nortest"
library(nortest)
## Fijamos la base de datos para utilizarla
attach(iris)
ad.test(Sepal.Length)##
## Anderson-Darling normality test
##
## data: Sepal.Length
## A = 0.8892, p-value = 0.02251Así, nuestro p valor es igual a 0.02251, con lo que podríamos concluir que nuestros datos NO siguen una distribución normal
- Prueba de Cramer-Von Mises
El Criterio de Cramer Von Mises, utiliza como criterio la distancia mínima de la función de distribución acumulada F en comparación con la función de distribución empírica Fn.
Es útil para pequeñas muestras y usa los momentos como criterio y es una alternativa a la prueba de Kolmogorov-Smirnov.
## Paquete "nortest"
## Crearemos una pequeña base
Sepal.Length2 <- Sepal.Length[1:10]
cvm.test(Sepal.Length2)##
## Cramer-von Mises normality test
##
## data: Sepal.Length2
## W = 0.036995, p-value = 0.7033Como nuestro p valor es igual a 0.7033 y por consiguiente mayor a 0.05 con lo que podríamos concluir que nuestros datos siguen una distribución normal
- Prueba de Lilliefors (Kolmogorov-Smirnov)
Utiliza la diferencia máxima absoluta entre la función de distribución acumulada empírica y la hipotética
Aunque el estadístico de prueba obtenido de lillie.text(x) es el mismo que el obtenido de ks(x,“pnorm”,mean(x),sd(x)), no es correcto usar el p-value de este último para la hipótesis compuesta de normalidad (media y varianza desconocidas), ya que la distribución del estadístico de prueba es diferente cuando se estiman los parámetros.
Se aplica más ampliamente cuando la muestra es grande.
## Paquete "nortest"
lillie.test(Sepal.Length)##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: Sepal.Length
## D = 0.088654, p-value = 0.005788Bajo este test nuestro p valor es igual a 0.005788, por lo que podríamos concluir que nuestros datos NO siguen una distribución normal
- Prueba de Pearson chi-square
Compara la distribución observada de los datos con una distribución esperada. La prueba de χ2 de Pearson generalmente no se recomienda para probar en la hipótesis compuesta de normalidad debido a sus propiedades de potencia son inferiores en comparación con otras pruebas.
Basada en una distribución χ2, que corresponde a una prueba de bondad de ajuste.
## Paquete "nortest"
pearson.test(Sepal.Length)##
## Pearson chi-square normality test
##
## data: Sepal.Length
## P = 17.4, p-value = 0.1352El resultado de nuestro p valor en este tipo es igual a 0.1352, con lo que podríamos concluir que nuestros datos siguen una distribución normal
- Prueba de Shapiro-Francia
La prueba de Shapiro-Francia es simplemente la correlación al cuadrado entre los valores de la muestra ordenados y los cuantiles esperados (aproximación) de la distribución normal estándar
Simplificación de la prueba Shapiro-Wilk y este tipo de prueba funciona bien, también el número de datos debe estar entre 5 y 5000.
## Paquete "nortest"
sf.test(Sepal.Length)##
## Shapiro-Francia normality test
##
## data: Sepal.Length
## W = 0.97961, p-value = 0.02621Así, nuestro p valor es igual a 0.02621, con lo que podríamos concluir que nuestros datos NO siguen una distribución normal
- Prueba de Frosini
La prueba de Frosini para la normalidad se basa en el siguiente estadístico:

## Paquete "normtest"
library(normtest)
frosini.norm.test(Sepal.Length, nrepl=2000)##
## Frosini test for normality
##
## data: Sepal.Length
## B = 0.2799, p-value = 0.0575El resultado de nuestro p valor es mayor a 0.05, con lo que podríamos concluir que nuestros datos siguen una distribución normal
- Prueba de Geary
La prueba de Geary se basa en el siguiente estadístico

Usa los valores acumulados muestrales, sus medias y desviaciones estándar
## Paquete "normtest"
geary.norm.test(Sepal.Length)##
## Geary test for normality
##
## data: Sepal.Length
## d = 0.8331, p-value = 0.02Por tanto, nuestro p valor es igual a 0.02, con lo que podríamos concluir que nuestros datos NO siguen una distribución normal
- Prueba de Hegazy-Green
La prueba de Hegazy-Green para la normalidad se basa en el siguiente estadístico:

## Paquete "normtest"
## nrepl: considera el número de replicas en simulación de Monte Carlo
hegazy1.norm.test(Sepal.Length, nrepl = 20000) ##
## Hegazy-Green test for normality
##
## data: Sepal.Length
## T = 0.098714, p-value = 0.03575Con este tipo de test nuestro p valor es menor a 0.05, con lo que podríamos concluir que nuestros datos NO siguen una distribución normal
- Prueba de Jarque-Bera Ajustada
La prueba de Jarque–Bera Ajustada para la normalidad se basa en el siguiente estadístico:

Utiliza un estadístico en la prueba que involucra la curtosis y la asimetría. – Usada por economistas.
## Paquete "normtest"
jb.norm.test(Sepal.Length, nrepl = 2000)##
## Jarque-Bera test for normality
##
## data: Sepal.Length
## JB = 4.4859, p-value = 0.0775El resultado para el p valor es igual mayor a 0.05, por lo que podríamos concluir que nuestros datos siguen una distribución normal
- Prueba de Kurtosis
La prueba de Kurtosis para la normalidad se basa en el siguiente estadístico:

## Paquete "normtest"
kurtosis.norm.test(Sepal.Length, nrepl = 2000)##
## Kurtosis test for normality
##
## data: Sepal.Length
## T = 2.4264, p-value = 0.1045Así, nuestro p valor es igual a 0.1045, con lo que podríamos concluir que nuestros datos siguen una distribución normal
- Prueba de Skewness
La prueba de Skewness para la normalidad se basa en el siguiente estadístico:

## Paquete "normtest"
skewness.norm.test(Sepal.Length, nrepl = 2000)##
## Skewness test for normality
##
## data: Sepal.Length
## T = 0.31175, p-value = 0.098Así, nuestro p valor es igual mayor a 0.05, con lo que podríamos concluir que nuestros datos siguen una distribución normal
- Prueba de Spiegelhalter
La prueba de Spiegelhalter para la normalidad se basa en el siguiente estadístico:

## Paquete "normtest"
spiegelhalter.norm.test(Sepal.Length, nrepl=2000)##
## Spiegelhalter test for normality
##
## data: Sepal.Length
## T = 1.2022, p-value = 0.9735Nuestro p valor es mayor a 0.05, con lo que podríamos concluir que nuestros datos siguen una distribución normal
- Prueba de Weisberg-Bingham
La prueba de Weisberg-Bingham para la normalidad se basa en el siguiente estadístico:

## Paquete "normtest"
wb.norm.test(Sepal.Length, nrepl=2000)##
## Weisberg-Bingham test for normality
##
## data: Sepal.Length
## WB = 0.97961, p-value = 0.0245Nuestro resultado para el p valor es mayor a 0.05, con lo que podríamos concluir que nuestros datos NO siguen una distribución normal
- Prueba de Agostino
La prueba de Agostino sirve para medir el nivel de asimetría de una normal en los datos. Bajo la hipótesis de la normalidad, los datos deben ser simétricos (es decir, la asimetría debe ser igual a cero).
## Paquete "moment"
library(moments)
agostino.test(Sepal.Length)##
## D'Agostino skewness test
##
## data: Sepal.Length
## skew = 0.31175, z = 1.59630, p-value = 0.1104
## alternative hypothesis: data have a skewnessAsí, nuestro p valor es igual a 0.1104, con lo que podríamos concluir que nuestros datos siguen una distribución normal
- Prueba de Shapiro-Wilk
La prueba de Shapiro-Wilk es ampliamente recomendada para la prueba de normalidad y proporciona una mejor potencia que K-S. Se basa en la correlación entre los datos y las puntuaciones normales correspondientes.
La prueba de normalidad es sensible al tamaño de muestra. Las muestras pequeñas con mayor frecuencia pasan las pruebas de normalidad. Por lo tanto, es importante combinar la inspección visual y la prueba de significación de normalidad para tomar la decisión correcta.
Es más poderosa cuando se compara con otras pruebas de normalidad cuando la muestra es pequeña.
shapiro.test(Sepal.Length)##
## Shapiro-Wilk normality test
##
## data: Sepal.Length
## W = 0.97609, p-value = 0.01018Así, nuestro p valor es igual a 0.01018, con lo que podríamos concluir que nuestros datos NO siguen una distribución normal
- Resumen normalidad
Visto los diferentes resultados de las pruebas realizadas para evidenciar normalidad, podemos inferir que los resultados dependerán en gran medida del tipo de test que elijamos usar. Y la pregunta del millón sería ¿entonces cuál debo utilizar? Pues no podemos darte una única respuesta, todo va a depender de tus datos, de la pregunta de investigación que quieras responder y la teoría detrás de cada análisis, porque es a partir de ello que tomaremos la mejor desición sobre que tipo de prueba es la más adecuada.

Sin embargo, la Prueba de Shapiro-Wilk es uno de los test más confiables y robustos, por lo que según sus resultados, nuestros datos NO se ajustarían a una distribución normal, por lo que hasta este momento, tendrémos que usar las pruebas para datos no paramétricos
Homocesdasticidad
La homocedasticidad en un modelo estadístico predictivo ocurre si en todos los grupos de datos de una o más observaciones, la varianza del modelo respecto de las variables explicativas (o independientes) se mantiene constante. Así, un modelo de regresión puede ser homocedástico o no, en cuyo caso se habla de heterocedasticidad. Una varianza constante nos permite disponer de modelos más fiables, además, si una varianza, aparte de ser constante es también más pequeña, nos dará como resultado una predicción del modelo más fiable.
La heterocedasticidad es, en estadística, cuando los errores no son constantes a lo largo de toda la muestra. El término es contrario a homocedasticidad.

En realidad es muy común observar que en un modelo de regresión aparezca la heterocedasticidad, ya que es complicado encontrar la variables perfectas desde el principio del experimento. Estos son algunos motivos que pueden producir heterocedasticidad
Contrastar la homocedasticidad de nuestros datos es en muchos test estadísticos una condición necesaria para poder ejecutarlos. Existen test para contrastar la homocedasticidad específicos para dos grupos (test F de Fisher) o para más de dos (test de Bartlett). Sin embargo, el test de Levene permite contrastar la homocedasticidad independientemente del número de grupos presentes. Es decir, lo puede ejecutar sobre dos o más de dos.
Existen diferentes test que permiten evaluar la distribución de la varianza. Todos ellos consideran como hipótesis nula que la varianza es igual entre los grupos y como hipótesis alternativa que no lo es. La diferencia entre ellos es el estadístico de centralidad que utilizan:
Los test que trabajan con la media de la varianza son los más potentes cuando las poblaciones que se comparan se distribuyen de forma normal.
Utilizar la media truncada mejora el test cuando los datos siguen una distribución de Cauchy (colas grandes).
La mediana consigue mejorarlo cuando los datos siguen una distribución asimétrica.
Por lo general, si no se puede alcanzar cierta seguridad de que las poblaciones que se comparan son de tipo normal, es recomendable recurrir a test que comparen la mediana de la varianza.
A continuación veremos algunos test para profundizar un poco más en el tema

- F-test
También conocido como contraste de la razón de varianzas, contrasta la hipótesis nula de que dos poblaciones normales tienen la misma varianza. Es muy potente, detecta diferencias muy sutiles, pero es muy sensible a violaciones de la normalidad de las poblaciones. Por esta razón, no es un test recomendable si no se tiene mucha certeza de que las poblaciones se distribuyen de forma normal.
Hagamos un ejercicio, esta vez lo haremos con la confiable base de datos
library(ggplot2)
library(dplyr)
## Cargamos la base de datos "iris"
data("iris")
## Filtramos los datos que utilizaremos
iris2 <- filter(iris, Species %in% c("versicolor", "virginica"))
dim(iris2)## [1] 100 5head(iris2)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 7.0 3.2 4.7 1.4 versicolor
## 2 6.4 3.2 4.5 1.5 versicolor
## 3 6.9 3.1 4.9 1.5 versicolor
## 4 5.5 2.3 4.0 1.3 versicolor
## 5 6.5 2.8 4.6 1.5 versicolor
## 6 5.7 2.8 4.5 1.3 versicolorAhora calculemos la varianza de la longitud del pétalo (Petal.Length) de las dos especies de plantas, I. versicolor e I. virginica)
aggregate(Petal.Length~Species, data = iris2, FUN = var)## Species Petal.Length
## 1 versicolor 0.2208163
## 2 virginica 0.3045878Ahora si hagamos la prueba
var.test(x = iris2[iris2$Species == "versicolor", "Petal.Length"],
y = iris2[iris2$Species == "virginica", "Petal.Length"] )##
## F test to compare two variances
##
## data: iris2[iris2$Species == "versicolor", "Petal.Length"] and iris2[iris2$Species == "virginica", "Petal.Length"]
## F = 0.72497, num df = 49, denom df = 49, p-value = 0.2637
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 0.411402 1.277530
## sample estimates:
## ratio of variances
## 0.7249678Así, de acuerdo al resultado anterior, p-value = 0.2637, podemos concluir que no se encuentra diferencias significativas entre las varianzas de los dos grupos, osea, tenemos un comportamiento de las varianzas en homocedasticidad.
- Test de Levene
El test de Levene se puede aplicar con la función
library(car)
leveneTest(y = iris2$Petal.Length, group = iris2$Species, center = "median")## Levene's Test for Homogeneity of Variance (center = "median")
## Df F value Pr(>F)
## group 1 1.0674 0.3041
## 98Así, de acuerdo al resultado anterior 0.3041, podemos concluir que no se encuentra diferencias significativas entre las varianzas de los dos grupos, osea, tenemos un comportamiento de las varianzas en homocedasticidad.
- Test de Bartlett
Permite contrastar la igualdad de varianza en 2 o más poblaciones sin necesidad de que el tamaño de los grupos sea el mismo. Es más sensible que el Test de Levene a la falta de normalidad, pero si se está seguro de que los datos provienen de una distribución normal, es la mejor opción.
## Organizamos los datos para realizar el test
a <- iris[iris$Species == "versicolor", "Petal.Length"]
b <- iris[iris$Species == "virginica", "Petal.Length"]
## Aplicamos el test
bartlett.test(list(a,b))##
## Bartlett test of homogeneity of variances
##
## data: list(a, b)
## Bartlett's K-squared = 1.249, df = 1, p-value = 0.2637Así, de acuerdo al resultado anterior, p-value = 0.2637, podemos concluir que no se encuentra diferencias significativas entre las varianzas de los dos grupos, osea, tenemos un comportamiento de las varianzas en homocedasticidad.
Ahora, si se aplica a los 3 grupos a la vez, sí hay evidencias de que la varianza no es la misma en todos ellos. Idea que se puede intuir a partir de sus gráficas (Fig. 5).
ggplot(iris, aes(x = Species, y = Petal.Length)) +
geom_boxplot(color = "black", fill = "steelblue")+
geom_jitter(alpha = 0.5)+
scale_y_continuous("Longitud del pétalo",
limits = c(0, 8),
breaks = seq(0, 8, by = 2))+
scale_x_discrete("Iris")+
theme(axis.title.y = element_text(size = 18),
axis.title.x = element_text(size = 18, face = "italic"),
axis.text.y = element_text(size = 16),
axis.text.x = element_text(size = 16, face = "italic"))+
theme(panel.border = element_blank(),
panel.grid.major = element_blank(),
panel.grid.minor = element_blank(),
axis.line = element_line(colour = "black", size = 1),
panel.background = element_blank())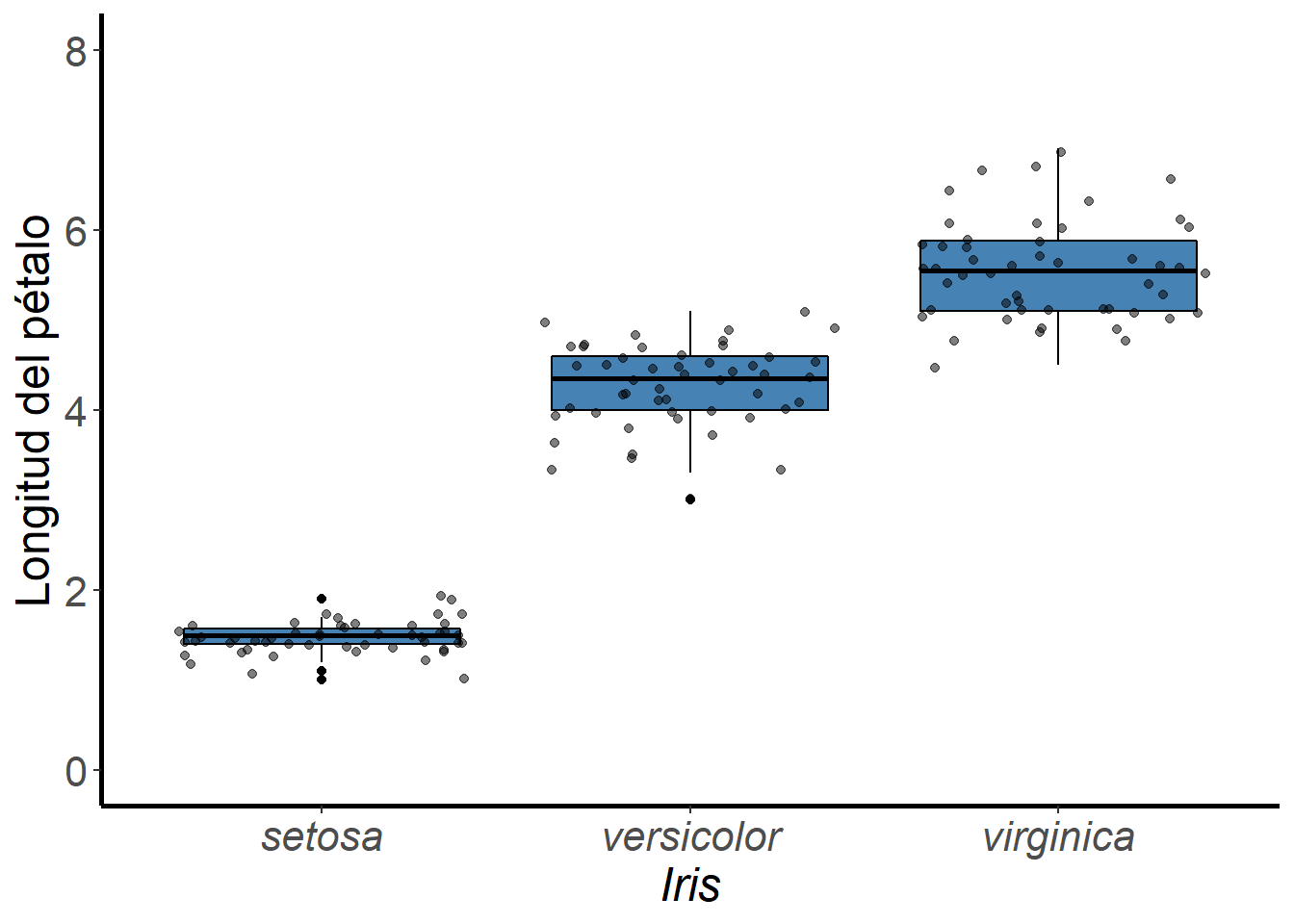
Fig. 5. Comportamiento de datos de la Longitud del pétalo para tres especies de plantas del género Iris.
Ahora organizamos nuestro datos para poder seguir con el ejercicio
## Calculamos la varianza respecto a las variables
aggregate(Petal.Length ~ Species, data = iris, FUN = var)## Species Petal.Length
## 1 setosa 0.03015918
## 2 versicolor 0.22081633
## 3 virginica 0.30458776## Y aplicamos el test
bartlett.test(iris$Sepal.Length ~ iris$Species)##
## Bartlett test of homogeneity of variances
##
## data: iris$Sepal.Length by iris$Species
## Bartlett's K-squared = 16.006, df = 2, p-value = 0.0003345Así, de acuerdo al resultado anterior, p-value = 0.0003345, podemos concluir que si se encuentran diferencias significativas entre las varianzas de los tres grupos, osea, tenemos un comportamiento de las varianzas en heterocedasticidad.
- Test de Brown-Forsythe
La prueba de Brown-Forsythe (B-F) se utiliza para probar el supuesto de varianzas iguales en ANOVA. Se puede encontrar dentro del paquete
library(onewaytests)
iris %>%
group_by(Species) %>%
summarize(Variance = var(Petal.Length))## # A tibble: 3 x 2
## Species Variance
## <fct> <dbl>
## 1 setosa 0.0302
## 2 versicolor 0.221
## 3 virginica 0.305bf.test(Petal.Length ~ Species, data = iris)##
## Brown-Forsythe Test (alpha = 0.05)
## -------------------------------------------------------------
## data : Petal.Length and Species
##
## statistic : 1180.161
## num df : 2
## denom df : 106.1748
## p.value : 3.016132e-73
##
## Result : Difference is statistically significant.
## -------------------------------------------------------------En nuestro ejemplo, se rechaza la hipótesis nula, por lo que podemos concluir que si se encuentran diferencias significativas entre las varianzas de los tres grupos, osea, tenemos un comportamiento de las varianzas en heterocedasticidad.
- Resumen Homocesdasticidad
Si tenemos la seguridad de que nuestras muestras siguen una distribución normal, son recomendables el F-test y el test de Bartlet, pareciendo ser el segundo más recomendable ya que el primero es muy potente pero extremadamente sensible a desviaciones de la normal.
Si no se tiene la seguridad de que las poblaciones de origen son normales, se recomiendan el Test de Leven utilizando la mediana.
Conclusión
Como pudimos leer y aprender, debemos hacer pruebas a nuestros datos para saber que tipo de pruebas podríamos aplicar a futuro, dependiendo si son datos paramétricos o no paramétricos. En la cual la normalidad y la homocesdasticidad de los datos, jugarán un papel importante, en la decisión personal a partir de los resultados de las pruebas de que tipo de datos tenemos.
Recuerda que las diferentes pruebas tienen un mismo objetivo, pero todas manejan ciertos critrios que dependerán de nuestros datos, nuestras preguntas de investigación y lo que en nuestro proceso de aprendizaje, podamos afirmar si es o no la prueba adecuada para nuestro estudio.

Así que los invitamos a seguir leyendo mucho más, recuerden que la intención de estos post no es más si no dar pequeñas pinceladas del amplio mundo de R en la biología.
No siendo más, muchas gracias por leernos y esperemos realmente, que de una u otra forma podamos contribuir al conocimiento de la ciencia.

Literatura citada
Más información
Estos análisis se han realizado utilizando el software R (v.4.1.0) y Rstudio (v. 1.4.1717)
Recuerda que todos nuestros códigos están almacenados en GitHub



