Se conoce como estadística paramétrica a las pruebas que se basan en el muestreo de una población con parámetros específicos como la normalidad y la homocedasticidad
Contenido del post
Introducción
Las pruebas paramétricas asumen distribuciones estadísticas subyacentes a los datos. Por tanto, deben cumplirse algunas condiciones de validez, de modo que el resultado de la prueba paramétrica sea fiable. Por ejemplo, la prueba t de Student para dos muestras independientes será fiable solo si cada muestra se ajusta a una distribución normal y si las varianzas son homogéneas.

Las ventajas de las pruebas paramétricas son:
- Sensibles a rasgos de los datos recolectados
- Estimaciones probabilísticas más exactas
- Tienen una mayor eficiencia estadística
- Mayor poder estadístico
Las desventajas de las purebas paramétricas son:
- Más complicadas de calcular
- Solo se pueden aplicar si se cumplen sus supuestos
Algunos de los análisis más populares son:
| Análisis | Paramétrico |
|---|---|
| Describir un grupo | μ - σ2 |
| Comparar un grupo a un valor | T Student de una muestra |
| Comparar medias en dos grupos | T Student de dos muestras |
| Comparar medias en dos grupos apareados | T Student apareada |
| Comparar medias en tres o más grupos | ANOVA |
| Correlación entre dos variables | Pearson (Lineal) |
Test Z
Se utiliza para determinar el grado de significatividad estadística de las diferencias entre las medias de dos conjuntos de datos. Se utiliza cuando las muestras son amplias (de más de 30 individuos aproximadamente) e independientes (esto es, no correlacionadas).
Cuando se tiene una población con distribución normal (o aproximada a la normal) y se conoce la varianza es posible emplear el estadístico Z para la prueba de hipótesis. Se parte del supuesto que H0: μ0 = μ1.

Recordemos que las varianzas son una medida de dispersión, es decir, qué tan dispersos están los datos con respecto a la media. Los valores más altos representan mayor dispersión.
Para realizar nuestra prueba de hipótesis con la función
z.test(
x, # Vector numérico; Se permiten NA e Inf, pero se eliminarán.
y = NULL, # Vector numérico; Se permiten NA e Inf, pero se eliminarán
alternative = "two.sided", # Indica la especificación de la hipótesis alternativa, "greater", "less" o "two.sided"
mu = 0, # Un solo número que representa el valor de la media o la diferencia en las medias especificadas por la hipótesis nula
sigma.x = NULL, # Un solo número que representa la desviación estándar de la población para x
sigma.y = NULL, # Un solo número que representa la desviación estándar de la población para y
conf.level = 0.95 # Nivel de confianza para el intervalo de confianza, restringido a estar entre cero y uno
)Veamos entonces algunos ejemplos con algunas consideraciones sobre nuestros datos
Una población normal con desviación estándar conocida
Se desea contrastar con un nivel de significancia del 5% la hipótesis de que la estatura media de los hombres de 18 o más años de un país es igual a 175, contra la alternativa que es menor que 175. Suponiendo que la desviación estándar es de 4.5.
Asumiremos que los datos tienen una distribución normal
# Cargamos el paquete
library(BSDA)
# Creamos nuestros datos
muestra <- c(167,167,168,168,168,169,171,172,173,175,175,175,177,182)
z.test(x = muestra,
alternative = "less",
mu = 175,
sigma.x = sd(muestra),
conf.level = 0.95)##
## One-sample z-Test
##
## data: muestra
## z = -2.5652, p-value = 0.005156
## alternative hypothesis: true mean is less than 175
## 95 percent confidence interval:
## NA 173.8981
## sample estimates:
## mean of x
## 171.9286Así, de acuerdo a nuestros resultados podemos rechazar Ho, ya que existe suficiente evidencia de que la estatura media de los hombres en ese país es menor que 175.
Dos poblaciones normales con varianzas conocidas
Un dueño de una fábrica tiene un pedido muy grande y para llevarlo a cabo necesita conocer cuál de las dos máquinas para realizar el proceso trabaja con mayor velocidad, el intuye que la maquina 2 es más efectiva y para ello hace una prueba, toman el tiempo de fabricación en minutos de 10 productos en cada máquina. ¿Es posible que la máquina 2 tenga un mejor tiempo de producción que la máquina 1 usando un nivel de significancia de 0.05?

Asumiremos que los datos tienen una distribución normal
Hipótesis:
- Ho: μ1 - μ2 = 0
- Ha: μ2 > μ1
maquina_1 <- c(14,13,15,14,17,16,15,16,13,17)
maquina_2 <- c(16,15,14,17,12,17,15,16,15,14)
z.test(x = maquina_1,
y = maquina_2,
alternative = "greater",
mu = 0,
sigma.x = sd(maquina_1), # sd() función para calcular desviación estándar
sigma.y = sd(maquina_2),
conf.level = 0.95)##
## Two-sample z-Test
##
## data: maquina_1 and maquina_2
## z = -0.14834, p-value = 0.559
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
## -1.208837 NA
## sample estimates:
## mean of x mean of y
## 15.0 15.1Como podemos observar en nuestros resultados, nuestra hipótesis nula fue rechazada, en su lugar nuestra hipótesis alternativa es aceptada, en conclusión, podemos decir que existe evidencia que la máquina 2 es más rápida que la máquina 1.
Test F
El test F de Fisher calcula la relación entre la varianza más grande y la varianza más pequeña. Usamos la prueba F cuando queremos verificar dónde las medias de tres o más grupos son diferentes o no. Se utiliza para evaluar si las varianzas de dos poblaciones (A y B) son iguales. Para ello utilizaremos la función
H0: σ12 = σ22 (Las varianzas poblacionales son iguales)
H1: σ12 ≠ σ22 (Las varianzas de población no son iguales)
var.test(formula, # Fórmula de la forma lhs ~ rhs donde lhs es una variable numérica que da los valores de los datos y rhs un factor con dos niveles que dan los grupos correspondientes.
data, # Matriz opcional o marco de datos que contiene las variables en la fórmula fórmula. Por defecto, las variables se toman del entorno (fórmula)
subset, # Vector opcional que especifica un subconjunto de observaciones que se utilizarán.
na.action) # Función que indica lo que debería suceder cuando los datos contienen NAVeamos un ejemplo, con las edades de los investigadores de dos grupos de estudio en la Universidad

# Definimos los dos grupos
data <- data.frame(valores = c(18, 19, 22, 25, 27, 28, 41, 45, 51, 55,
14, 15, 15, 17, 18, 22, 25, 25, 27, 34),
grupo = rep(c('A', 'B'), each = 10))
# Realizamos un F-test para determinar si las varianzas son iguales
var.test(valores ~ grupo, data = data)##
## F test to compare two variances
##
## data: valores by grupo
## F = 4.3871, num df = 9, denom df = 9, p-value = 0.03825
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
## 1.089699 17.662528
## sample estimates:
## ratio of variances
## 4.387122Así, el estadístico de la prueba F es 4.3871 y el valor p correspondiente es 0.03825. Dado que este valor p es menor que .05, rechazaríamos la hipótesis nula. Esto significa que, tenemos suficiente evidencia para decir que las dos variaciones de población NO son iguales.
Test T de student
Es un estadístico para comparar la media de una muestra (x̄) con la de la población (μ) sin necesidad de conocer su varianza (σ). El hecho de que los valores promedio de cada grupo no sean iguales no implica que haya evidencias de una diferencia significativa. Dado que cada grupo tiene su propia variabilidad, aunque el tratamiento no sea eficaz, las medias muestrales no tienen por qué ser exactas. Este test fue desarrollado por William Sealy Gosset, mejor conocido por su pseudónimo Student.

Para utilizar la t de Student es necesario que se cumplan los siguientes supuestos:
- La muestra es aleatoria
- Se desconoce la σ
- Los datos tienen una distribución normal o n ≥ 30
- Los errores tienen una distribución normal
- Cuando se comparan dos distribuciones las varianzas son iguales (σ1 = σ2)
La función requerida para este cálculo es
t.test(x, y = NULL, # Un vector numérico (no vacío) de valores de datos
alternative = c("two.sided", "less", "greater"), # Especificando la hipótesis alternativa
mu = 0, # Número que indica el valor real de la media (o la diferencia de medias si está realizando una prueba de dos muestras).
paired = FALSE, # Un indicador lógico que indica si desea una prueba t emparejada.
var.equal = FALSE, # Variable lógica que indica si se deben tratar las dos varianzas como iguales
conf.level = 0.95) # Nivel de confianza del intervalo.Test T de student para una muestra
Permite comprobar si es posible aceptar que la media de la población es un valor determinado. Se toma una muestra y el Test permite evaluar si es razonable mantener la Hipótesis nula de que la media es tal valor.
Se trata de un test paramétrico; o sea, parte de la suposición de que la variable analizada en el conjunto de la población sigue una variabilidad, una distribución como la de la campana de Gauss. Por lo tanto, podemos pensar que la distribución normal es un buen modelo de esa población.
Para este ejemplo utilizaremos la variable largo del sépalo (sepal.lenght) de la especie I. setosa de la base Iris, asumiendo que cumple con los criterios establecidos para este tipo de test, como lo vimos en nuestro anterior POST

Así, asumiremos que un investigador propone que a partir de sus observaciones considera que la longitud del sépalo de I. setosa es de 5.3cm
# Filtamos la información para nuestro ejercicio
datos <- iris[iris$Species == "setosa", ]$Sepal.Length
t.test(datos,
alternative = "two.sided",
mu = 5.3,
conf.level = 0.95)##
## One Sample t-test
##
## data: datos
## t = -5.8977, df = 49, p-value = 3.363e-07
## alternative hypothesis: true mean is not equal to 5.3
## 95 percent confidence interval:
## 4.905824 5.106176
## sample estimates:
## mean of x
## 5.006Por tanto, el resultado nos presenta que la media teórica no corresponde a los datos que se estudiaron. El valor de la media con un intervalo de confianza del 95% situa a la media entre los valores de 4.905824 y 5.106176, con una media aritmética de 5.006, por lo cual la propuesta del investigador es inválida.
Test T de student para dos muestras de medias poblacionales independientes
Para realizar este tipo de análisis las observaciones tienen que ser independientes unas de las otras. Para ello el muestreo debe ser aleatorio y el tamaño de la muestra inferior al 10% de la población.
Los pasos a seguir para realizar un t-test de medias independientes son:
- Establecer las hipótesis
Hipótesis nula (Ho): por lo general es la hipótesis escéptica, la que considera que no hay diferencia o cambio. Suele contener en su definición el símbolo =. En el caso de comparar dos medias independientes la hipótesis nula considera que μ1 = μ2.
Hipótesis alternativa (Ha): considera que el valor real de la media poblacional es mayor, menor o distinto del valor que establece la Ho. Suele contener los símbolos >, <, ≠. En el caso de comparar dos medias independientes la hipótesis alternativa considera que μ1 ≠ μ2.
- Calcular el estadístico (parámetro estimado)
El estadístico es el valor que se calcula a partir de la muestra y que se quiere extrapolar a la población de origen. En este caso es la diferencia de las medias muestrales (x̄1 - x̄2).
- Determinar el tipo de test, una o dos colas
Los test de hipótesis pueden ser de una cola o de dos colas. Si la hipótesis alternativa emplea “>” o “<” se trata de un test de una cola, en el que solo se analizan desviaciones en un sentido. Si la hipótesis alternativa es del tipo “diferente de” se trata de un test de dos colas, en el que se analizan posibles desviaciones en las dos direcciones. Solo se emplean test de una cola cuando se sabe con seguridad que las desviaciones de interés son en un sentido y únicamente si se ha determinado antes de observar la muestra, no a posteriori.

Ejemplo
Ahora, exploraremos la relación entre las especies del género Iris (species) y el largo de su sépalo (Sepal.Length) de la base de datos Iris. Una es una variable categórica y la otra es una variable continua. Para tener una idea rápida de si uno afecta al otro, podemos mirar el diagrama de caja y en la cual asumiremos que cumplen con los criterios que deben cumplir para hacer un test paramétrico como lo vimos en nuestro anterior POST
# Cargamos las librerías necesarias
library(ggplot2)
# Filtramos la información, vamos a eliminar los datos de la especie I. virginica y observamos los datos
datos2 <- iris[iris$Species != "virginica",]
head(datos2)## Sepal.Length Sepal.Width Petal.Length Petal.Width Species
## 1 5.1 3.5 1.4 0.2 setosa
## 2 4.9 3.0 1.4 0.2 setosa
## 3 4.7 3.2 1.3 0.2 setosa
## 4 4.6 3.1 1.5 0.2 setosa
## 5 5.0 3.6 1.4 0.2 setosa
## 6 5.4 3.9 1.7 0.4 setosa# Recuerda que la base Iris está por defecto en un computadora
ggplot(datos2, aes(x = Species, y = Sepal.Length)) +
geom_boxplot() +
labs(x = "Especies",
y = "Largo del sépalo")+
theme_bw()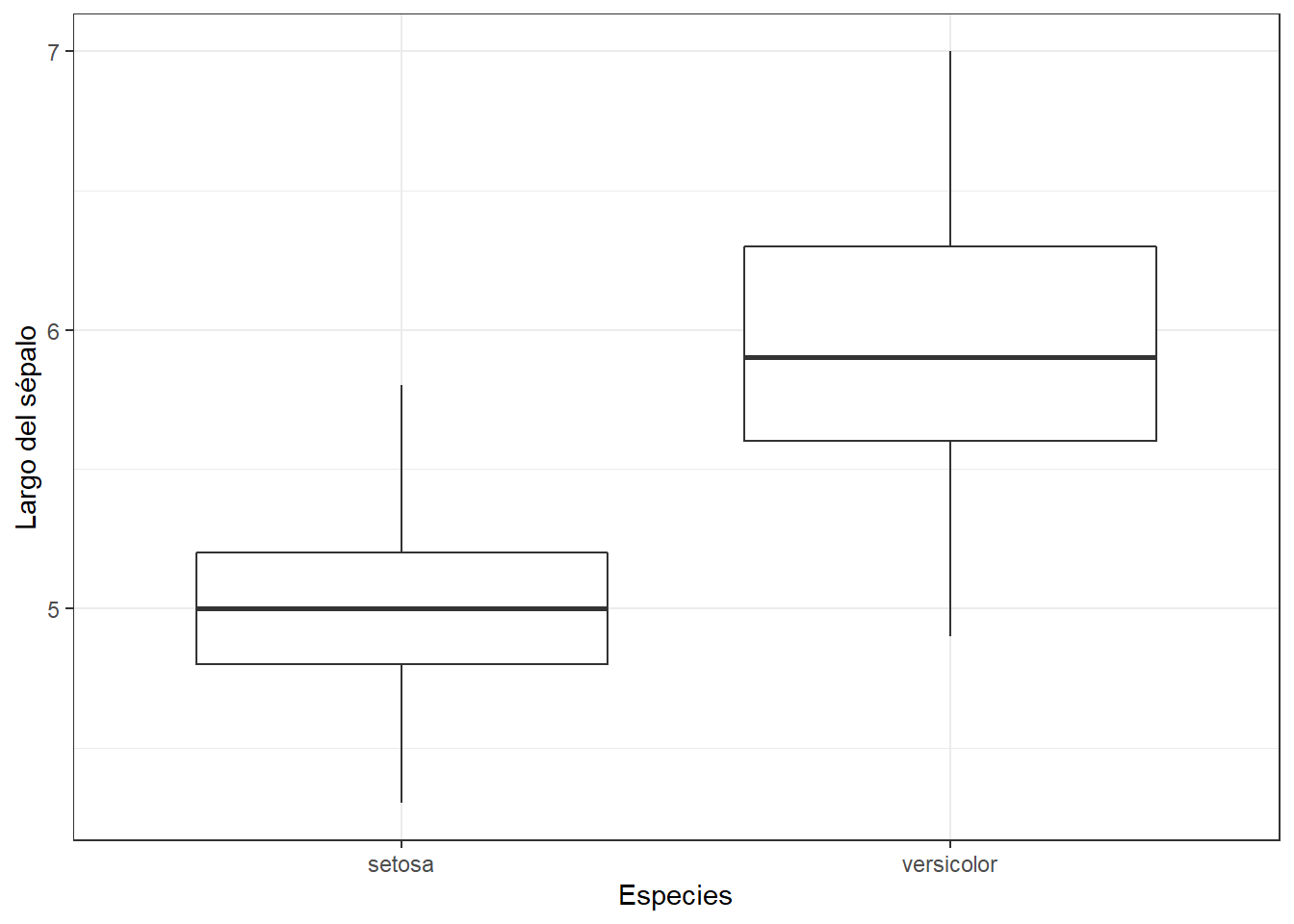
Ahora calculemos el p valor a partir del estadístico t student. R tiene una función integrada que permite realizar t-test para una o dos muestras, tanto con corrección (en caso de que las varianzas no sean iguales) como sin ella. Esta función devuelve tanto el p-value del test como el intervalo de confianza para la verdadera diferencia de medias.
# Filtramos la información para realizar el test
x <- iris[iris$Species == "setosa", ]$Sepal.Length
y <- iris[iris$Species == "versicolor", ]$Sepal.Length
t.test(x,
y,
paired = FALSE,
alternative = "two.sided",
var.equal = FALSE)##
## Welch Two Sample t-test
##
## data: x and y
## t = -10.521, df = 86.538, p-value < 2.2e-16
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## -1.1057074 -0.7542926
## sample estimates:
## mean of x mean of y
## 5.006 5.936Como podemos observar en los resultados anteriores, el valor de p es 2.216 es significativamente más bajo que nuestro umbral del 5%. Por tanto, podemos rechazar la hipótesis nula y aceptar la alternativa.
Según la hipótesis alternativa, los valores de Sepal.Length para varias especies son estadísticamente diferentes entre sí, es decir, los valores están claramente separados entre las diferentes clases de especies.
Test T de student para dos muestras de medias poblacionales dependientes (pareadas)
Dos medias son dependientes o pareadas cuando proceden de grupos o muestras dependientes, esto es, cuando existe una relación entre las observaciones de las muestras. Este escenario ocurre a menudo cuando los resultados se generan a partir de los mismos individuos bajo condiciones distintas.
Las pruebas pareadas tienen la ventaja frente a los independientes de que se puede controlar mejor la variación no sistematica, ya que se bloquean al estar examinando los mismos individuos dos veces, no dos grupos de individuos distintos.

Veamos un ejemplo, donde el programa de biología ha decidido contratar a un nuevo profesor para un grupo de estudio. Para decidir si al cabo de un año mantienen su contrato se selecciona aleatoriamente a 10 estudiantes y se resgistran sus avances en el proyecto (0 a 5, donde 5 es la mayor nota) al inicio del año, al final del año se volverá a registrar esos mismos 10 estudiantes. En vista de los datos obtenidos ¿Hay diferencia significativa entre el rendimiento de los estudiantes tras un año de estudiar con el nuevo profesor?
# Creamos las variables deseadas
notas <- data.frame(
estudiante = c(1:10),
antes = c(2.9, 3.5, 2.8, 4.5, 3.7, 2.9, 2.6, 3.5, 4.4, 1.3),
despues = c(2.7, 3.6, 2.0, 4.2, 3.6, 2.0, 2.0, 3.5, 4.6, 1.1)
)
head(notas)## estudiante antes despues
## 1 1 2.9 2.7
## 2 2 3.5 3.6
## 3 3 2.8 2.0
## 4 4 4.5 4.2
## 5 5 3.7 3.6
## 6 6 2.9 2.0Al tratarse de datos pareados, interesa conocer la diferencia en cada par de observaciones, al igual que otros ejemplos asumiremos el cumplimiento de los supuestos par pruebas paramétricas.
R contiene la función
t.test(x = notas$antes,
y = notas$despues,
alternative = "two.sided",
mu = 0,
paired = TRUE, # Datos pareados
conf.level = 0.95)##
## Paired t-test
##
## data: notas$antes and notas$despues
## t = 2.3702, df = 9, p-value = 0.0419
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.01276315 0.54723685
## sample estimates:
## mean of the differences
## 0.28Como el p-value > α, no hay evidencias estadísticas significativas para rechazar H0 en favor de HA. Por lo tanto, no se pude considerar que el rendimiento de los estudiantes haya cambiado, al parecer este profe no conservará su puesto.
Test T de Student para dos muestras independientes con varianzas no homogéneas
Para este ejemplo vamos a suponer que nuestros datos anteriores son muestras normales pero no tienen varianzas iguales. Por ello, procederemos a realizar el test de Welch. Los siguientes vectores muestran los puntajes de los exámenes de los estudiantes de cada grupo
booklet <- c(90, 85, 88, 89, 94, 91, 79, 83, 87, 88, 91, 90)
no_booklet <- c(67, 90, 71, 95, 88, 83, 72, 66, 75, 86, 93, 84)
t.test(booklet,
no_booklet)##
## Welch Two Sample t-test
##
## data: booklet and no_booklet
## t = 2.2361, df = 14.354, p-value = 0.04171
## alternative hypothesis: true difference in means is not equal to 0
## 95 percent confidence interval:
## 0.3048395 13.8618272
## sample estimates:
## mean of x mean of y
## 87.91667 80.83333De nuestros resultados podemos ver que el estadístico de prueba t es 2.2361 y el valor p correspondiente es 0.04171.
Dado que este valor p es menor que .05, podemos rechazar la hipótesis nula y concluir que existe una diferencia estadísticamente significativa en las puntuaciones medias de los exámenes entre los dos grupos.
Resumen
Como pudimos leer en este post, hay varios estadísticos que nos permitirán tratar nuestros datos paramétricos, recordemos que deben cumplir ciertos criterios para ser llamados de esta manera.
En nuestro próximo post veremos otro análisis muy importante como lo es el Análisis de Varianzas o conocido como ANOVA.
Hasta pronto y gracias por acompañarños, recuerda que si tienes alguna duda o comentario, nos puedes escribir a través de nuestras redes sociales o nuestro correo
¡¡¡Hasta pronto!!!

Bibliografía
Más información
Estos análisis se han realizado utilizando el software R (v.4.1.0) y Rstudio (v. 1.4.1717)
Recuerda que todos nuestros códigos están almacenados en GitHub


