Contenido del post

• Introducción
• Regresión lineal simple
• Correlación lineal
  • Correlación de Pearson
  • coeficiente de determinación
  • Gráfico de correlaciones
• Resumen
• Bibliografía
• Anexos
• Más información

Introducción

La regresión lineal es una técnica de modelado estadístico que se emplea para describir una variable de respuesta continua como una función de una o varias variables predictoras. Puede ayudar a comprender y predecir el comportamiento de sistemas complejos o a analizar datos biológicos.

A continuación veremos algunas formas de la regresión con algunos ejemplos para que practiques

Regresión lineal simple

En un modelo de regresión lineal simple tratamos de explicar la relación que existe entre la variable respuesta Y y una única variable explicativa X.

Para trabajar el modelo de regresión lineal simple, es necesario trabajar con la función lm(), con los argumentos que vamos a mostrar a continuación, sin embargo, podemos tener más información de la función en este LINK

lm(formula, # Objeto de clase 'fórmula': una descripción simbólica del modelo que se va a ajustar.
   data, # Marco de datos, lista o entorno opcional que contiene las variables en el modo
   na.action) # Función que indica lo que debería suceder cuando los datos contienen NA

vamos a poner en contexto una situación en donde tenemos las especies de plantas Iris. En este caso, nos va a interesar conocer la relación entre el largo del sépalo y el largo del pétalo.

# Cargamos el paquete dplyr para organizar los datos y ggplot2 para graficar
library(dplyr)
library(ggplot2)
data("iris")

# Veamos el comportamiento de los datos en una gráfica
iris %>% 
        ggplot(aes(x = Sepal.Length,
                   y = Petal.Length)) +
        geom_point()+
        theme_bw()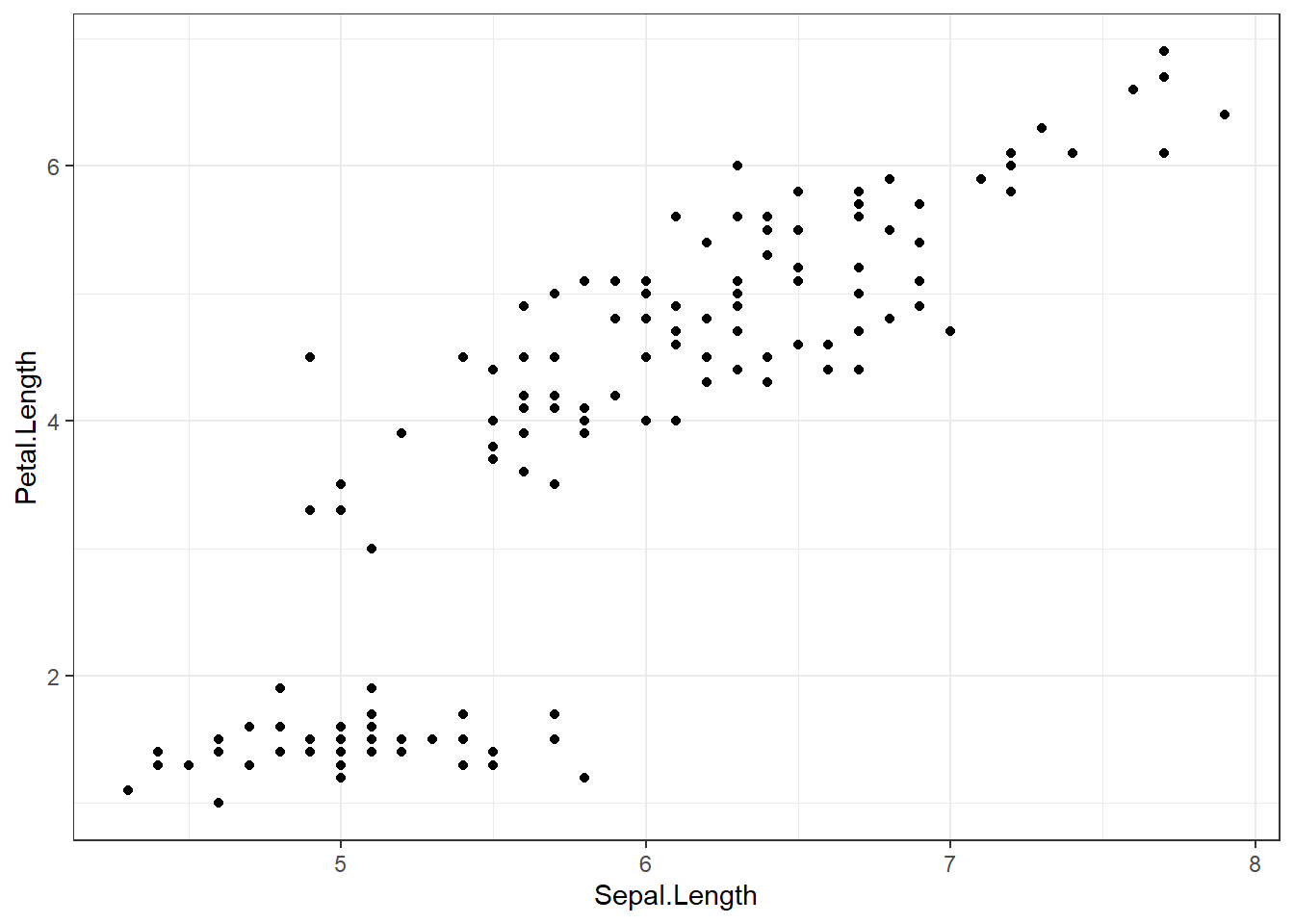

Como podemos observar en este gráfico la tendencia lineal es clara, sin embargo, es necesario encontrar los valores estadísticos para afirmar este comportamiento.

modelo_lineal <- lm(Sepal.Length ~ Petal.Length, # De esta manera se formula la relación entre dos variables
                    data = iris)

summary(modelo_lineal)

## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length, data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.24675 -0.29657 -0.01515  0.27676  1.00269 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   4.30660    0.07839   54.94   <2e-16 ***
## Petal.Length  0.40892    0.01889   21.65   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4071 on 148 degrees of freedom
## Multiple R-squared:   0.76,  Adjusted R-squared:  0.7583 
## F-statistic: 468.6 on 1 and 148 DF,  p-value: < 2.2e-16

Mediante este ejemplo podemos interpretar varios valores mostrados en el summary. Empecemos, el valor de R² indica que el modelo calculado explica el 76% de la variabilidad presente en la variable respuesta (Ancho del sépalo) mediante la variable independiente (Largo del sépalo), con un p-value de 2.2e-16) el cual determina que sí es significativamente superior la varianza explicada por el modelo en comparación a la varianza total. Es el parámetro que determina si el modelo es significativo y por lo tanto se puede aceptar la veracidad del modelo.

Alternativamente, podemos agregar a nuestro gráfico la línea de tendencia lineal de nuestro modelo, mediante la función geom_smooth() para poder observar el comportamiento de nuestros resultados y verificarlos

ggplot(data = iris, mapping = aes(x = Sepal.Length, y = Petal.Length)) +
        geom_point() +
        labs(x = "Largo del sépalo", y = "Largo del pétalo") +
        geom_smooth(method = "lm", se = FALSE, color = "red") +
        theme_bw()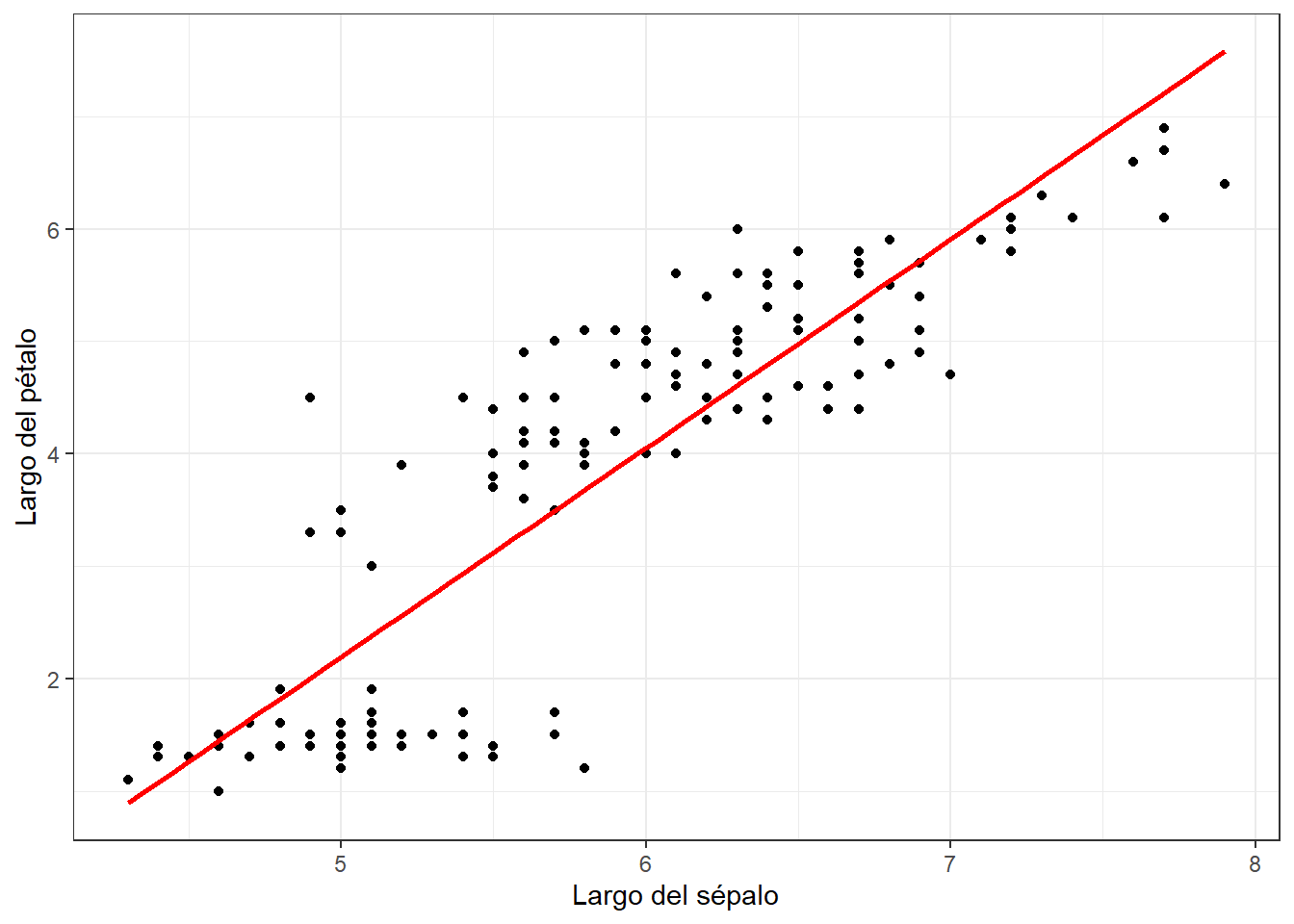

De esta manera, podemos observar que nuestra línea de tendencia tiene cierto comportamiento en relación a la nube de puntos de la relación de nuestros datos, por lo cual, podemos inferir que nuestro modelo de regresión lineal si se está cumpliendo.

Correlación lineal

En ocasiones nos puede interesar estudiar si existe o no algún tipo de relación entre dos variables aleatorias. Las relaciones o asociaciones de este tipo entre variables se denominan correlaciones; y están medidas en escalas ordinales o de intervalos. En particular, nos interesa cuantificar la intensidad de la relación lineal entre dos variables.

Un coeficiente de correlación mide el grado en que dos variables tienden a cambiar al mismo tiempo. Cuando el aumento de una de las variables viene acompañado del aumento de la otra, se trata de una correlación positiva o directa y viceversa. Una Correlación perfecta se da cuando todos los puntos de un diagrama de dispersión forman una linea recta perfecta. Estas correlaciones perfectas (positivas o negativas) prácticamente no existen en biología.

Los coeficientes de correlación describen tanto la fuerza como la dirección de la relación y se pueden calcular mediante métodos paramétricos y no paramétricos. Y su calculo en R se puede hacer a través de la función cor().

La correlación nos indica el signo y magnitud de la tendencia entre dos variables.

El signo nos indica la dirección de la relación

– Un valor positivo indica una relación directa o positiva,

– Un valor negativo indica relación inversa o negativa,

– Un valor nulo indica que no existe una tendencia entre ambas variables (puede ocurrir que no exista relación o que la relación sea más compleja que una tendencia, por ejemplo, una relación en forma de U).

– La magnitud nos indica la fuerza de la relación, que toma valores entre -1 a 1.

Cuanto más cercano sea el valor a los extremos del intervalo (1 o -1) más fuerte es la tendencia de las variables, o menor es la dispersión existe en los puntos alrededor de dicha tendencia. Cuanto más cercano sea a 0 sea el coeficiente de correlación, más débil será la tendencia, es decir, más dispersión habrá en la nube de puntos, como vemos en esta gráfica explicativa.

cor(x, y, use = "everything",
    method = c("pearson", "kendall", "spearman"))

Los parámetos de la función son:

• x, y: vectores cuantitativos.
• use: parámetro que indica lo que se debe hacer cuando se presenten registros NA en alguno de los vectores. Las diferentes posibilidades son: everything, all.obs, complete.obs, na.or.complete y pairwise.complete.obs, el valor por defecto es everything.
• method: tipo de coeficiente de correlación a calcular, por defecto es pearson, otros valores posibles son kendall y spearman.

¡¡¡Atención, atención!!!

Ten en cuenta que si tus datos contienen valores perdidos, deberas usar el siguiente código R para manejar los valores perdidos mediante la eliminación por caso.

cor(data, use = "complete.obs")

Antes de continuar, para saber que tipo correlación aplicar es importante revisar los supuestos de las pruebas, en este ejercicio haremos las pruebas bajo el test de Normalidad de Shapiro-Wilk, como lo vimos en nuestro post Supuestos estadísticos. Si nuestros datos presentan una distribución normal, la Correlación de Pearson es la prueba adecuada para nuestros datos.

Correlación de Pearson

Es un coeficiente paramétrico que evalúa la relación lineal entre dos variables continuas. Una relación es lineal cuando un cambio en una variable se asocia con un cambio proporcional en la otra variable.

Para este ejemplo usaremos la base de datos Datos escarabajos, la cual contiene los datos de un estudio de Escarabajos coprófagos y sus funciones ecológicas.

Descarga aquí

Usaremos las variables Individuos y Dispersión, con el fin de encontrar su posible correlación. Primero realizamos el test de Normalidad, con el fin de saber que tipo de prueba de correlación vamos a realizar.

url <- "https://raw.githubusercontent.com/davidvaneal/Documentos-RBiologos/main/Datos%20escarabajos.csv"
esc <- read.csv(url)

shapiro.test(esc$Especies)

## 
##  Shapiro-Wilk normality test
## 
## data:  esc$Especies
## W = 0.88433, p-value = 0.1743

shapiro.test(esc$Dispersión)

## 
##  Shapiro-Wilk normality test
## 
## data:  esc$Dispersión
## W = 0.91145, p-value = 0.3261

De acuerdo a nuestros resultados tenemos una distribución normal para nuestras variables, por lo que podemos usar una Correlación de Pearson para evaluar si la riqueza de especies de los escarabajos tiene relación con la tasa de semillas dispersadas por estos (%).

cor.test(esc$Especies, esc$Dispersión,
    method = c("pearson"))

## 
##  Pearson's product-moment correlation
## 
## data:  esc$Especies and esc$Dispersión
## t = 6.4253, df = 7, p-value = 0.0003586
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.6751838 0.9843259
## sample estimates:
##       cor 
## 0.9246766

Del resultado anterior vemos que existe una correlación de 0.9246766 entre las dos variables, lo que quiere decir que si hay relaciones estadísticas significativas entre la riqueza de especies de escarabajos coprófagos y la tasa de semillas dispersadas.

Ahora observemos el comportamiento de los puntos en una gráfica (Fig. 1), mediante el paquete ggplot2.

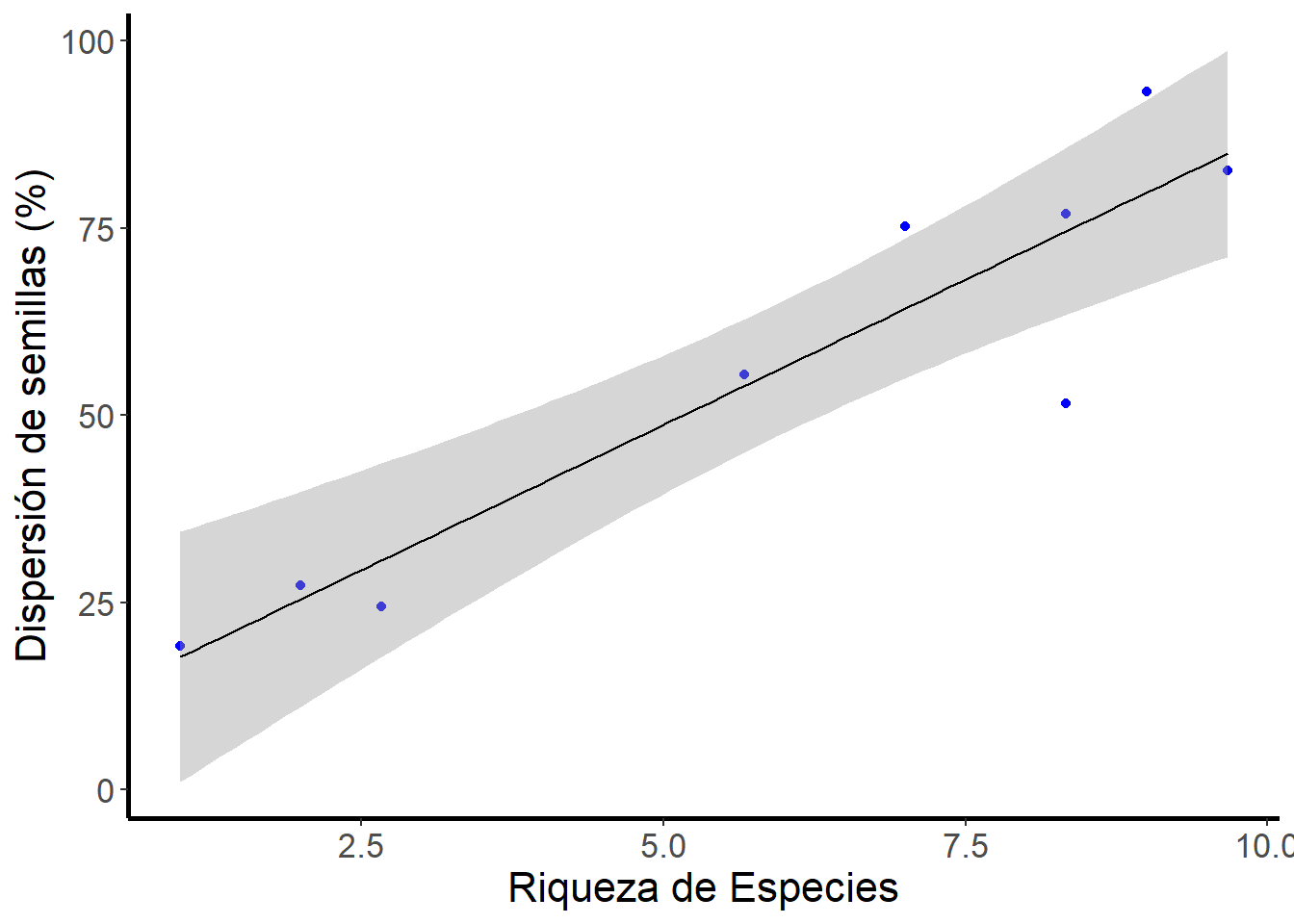
Fig. 1. Riqueza de especies de escarabajos prófagos y la tasa de semillas dispersadas por parte de estos Anexo 1.

Claramente se observa un patrón de relación de la nube de puntos (Fig. 1), estos puntos no se observan dispersos y por tanto el valor del coeficiente de correlación.

Coeficiente de determinación

El cuadrado del coeficiente de correlación de Pearson es, en si mismo, un estadístico de gran utilidad denominado coeficiente de determinación. Es una medida de la proporción de la variabilidad en una variable, atribuible a la variabilidad de la otra.

En otras palabras, ¿cual es la proporción de la variación total en Y que puede ser explicada por la variación en X?

Para este ejercicio tomaremos el valor de correlación del ejercicio anterior

coeffdet <- 0.9246766^2
coeffdet

## [1] 0.8550268

Así podemos deducir que aproximadamente el 85.50% de la riqueza de especies de los escarabajos está relacionado con la tasa de semillas dispersadas.

Gráfico de correlaciones

Es posible representar gráficamente las matrices de correlaciones por medio de la función corrplot del paquete corrplot (Para obtener mayor información puedes consultar la siguiente página An Introduction to corrplot Packaged.

Para realizar este ejercicio vamos a utilizar los resultados de la correlación de la base de datos Escarabajos y todas sus variables, analizando en primera instancia su normalidad.

lapply(esc, shapiro.test)

## $Individuos
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.96509, p-value = 0.8498
## 
## 
## $Especies
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.88433, p-value = 0.1743
## 
## 
## $Biomasa
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.82405, p-value = 0.03828
## 
## 
## $Longitud
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.87821, p-value = 0.1504
## 
## 
## $Heces
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.92558, p-value = 0.4405
## 
## 
## $Suelo
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.8997, p-value = 0.2503
## 
## 
## $Dispersión
## 
##  Shapiro-Wilk normality test
## 
## data:  X[[i]]
## W = 0.91145, p-value = 0.3261

Como podemos ver la única variable que no cumple con el supuesto de normalidad es Biomasa. Por lo que vamos a realizar nuestro análisis de correlación sin dicha variable.

## Eliminamos la variable "Biomasa"
esc2 <- esc[,-3]

## Cargamos el paquete para generar nuestro gráfico
library(corrplot)

## Seguimos con el análisis
esc.cor <-round(cor(esc2), 4)
esc.cor

##            Individuos Especies Longitud   Heces   Suelo Dispersión
## Individuos     1.0000   0.8153   0.0896  0.8803  0.8847     0.9576
## Especies       0.8153   1.0000  -0.0105  0.8578  0.8572     0.9247
## Longitud       0.0896  -0.0105   1.0000 -0.1028 -0.1040     0.0066
## Heces          0.8803   0.8578  -0.1028  1.0000  0.8150     0.9335
## Suelo          0.8847   0.8572  -0.1040  0.8150  1.0000     0.9322
## Dispersión     0.9576   0.9247   0.0066  0.9335  0.9322     1.0000

Y finalmente podemos hacer uso de las herramientas gráficas para poder visualizar de una manera más visual nuestros resultados

## Definimos colores
col <- colorRampPalette(c("#BB4444", "#EE9988", "#FFFFFF",
                          "#77AADD", "#4477AA"))
## Y graficamos
corrplot(esc.cor, method = "shade", sade.col = NA, tl.col = "black", 
         tl.srt = 45, col = col(200), addCoef.col = "black", 
         addcolorlabel = "no", order = "AOE", type = "upper", diag = F)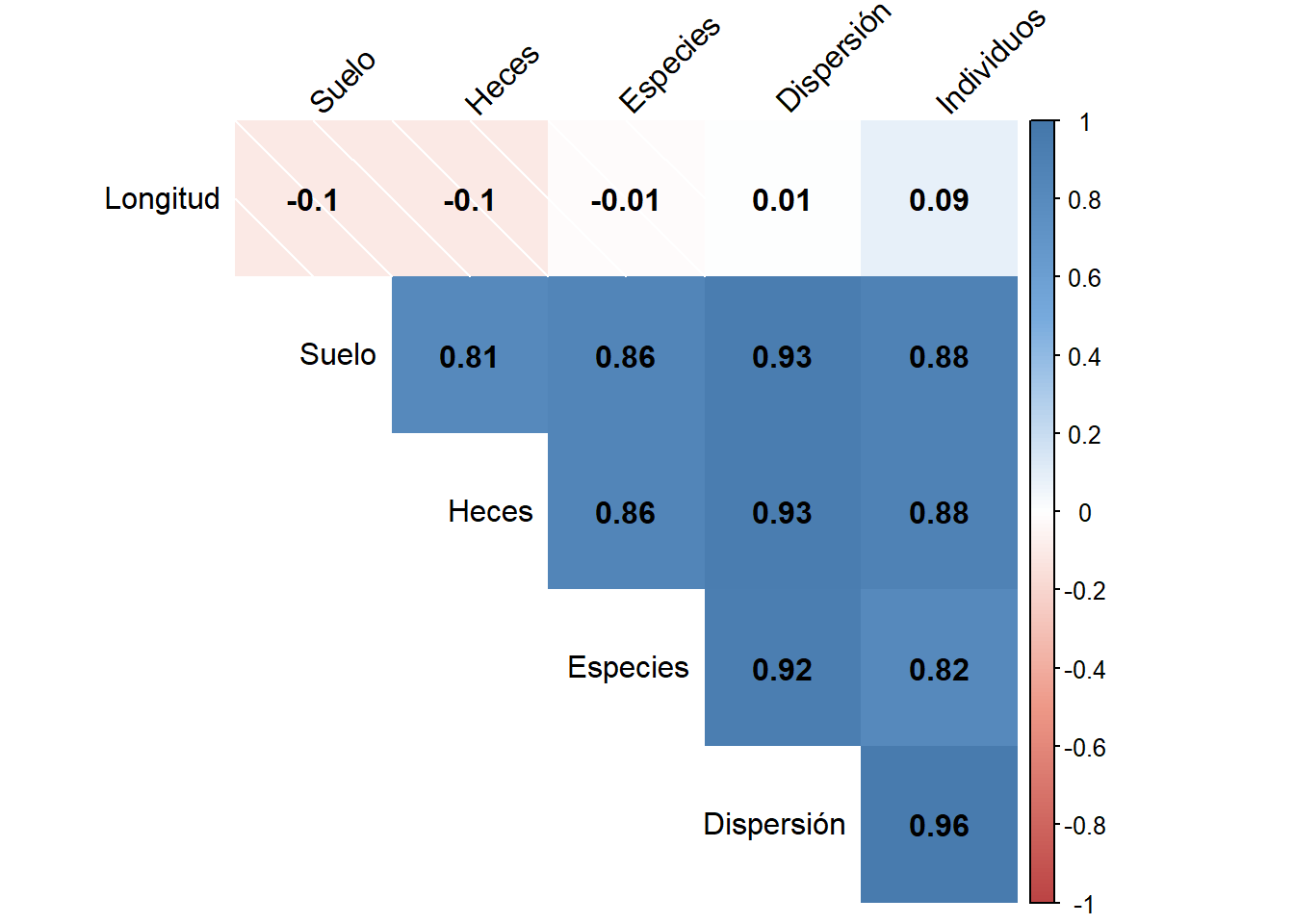

En este tipo de gráficos en la diagonal están las variables, por encima están los cuadros de colores, entre más intensidad del color, ya sea azul (positiva) o rojo (negativa), mayor es la correlación, donde los colores ténues significan correlación baja. Dentro de cada cuadro se observan los valores exactos de correlación.

Como podemos observar en nuestro gráfico, se muestra la matriz con los coeficientes de correlación entre todas las variables, siendo la correlación más fuerte entre la tasa de dispersión de semillas y el número de individuos, y la más baja entre la tasa de dispersión de semillas y la longitud de los escarabajos.

Resumen

Evidenciar una relación lineal entre dos variables parece ser sencillo bajo lo aprendido el día de hoy, sin embargo, es muy importante saber que detrás de todo ello hay matemática pura y dura que debemos tener muy en cuenta. Nosotros solamente te damos un pequeño empujón en el mundo de R, así que debes investigar y leer mucho más sobre estos temas.

Pudimos aprender un poco más sobre las relaciones paramétricas como las regresiones lineales simples y la correlación de Pearson. Sobre las regresiones lineales estudiamos los valores de sus resultados y como poder graficar para poder observar dicho comportamiento, recuerda que debemos observar y tener en cuenta nuestras gráficas y nuestros resultados para dar un dictamen más robusto. Asimismo, sobre la correlación de Pearson estudiamos sobre los signos y magnitudes de los resultados y como poder graficar dichos valores de resultados.

Muchas gracias por leernos, esperamos puedan aprender tanto como nosotros en este post ¡hasta pronto!

Ahhhh y aprovechamos para desearles una muy ¡¡¡Feliz Navidad!!!, que esta festividad sea un símbolo de amor y paz en el corazón de todo el mundo, con grandes aprendizajes y momentos felices en familia y amigos, brindando por los que no pueden estar y los que vendrán.

Bibliografía

• Correlación lineal y Regresión lineal simple

• Correlación y Regresión Lineal

• Medidas de correlación

• Coeficientes de correlación

• Correlación

Anexos

Anexo 1

ggplot(esc, aes(x = Individuos, y = Dispersión))+
      geom_point(col='blue')+
      scale_y_continuous("Dispersión de semillas (%)")+
      scale_x_continuous("Longitud escarabajos (mm)")+
      theme(axis.title.y = element_text(size = 16),
            axis.title.x = element_text(size = 16),
            axis.text.y = element_text(size = 13),
            axis.text.x = element_text(size = 13))+
      theme(panel.background = element_blank(), 
            panel.border = element_blank(),
            panel.grid.major = element_blank(),
            panel.grid.minor = element_blank(),
            axis.line = element_line(colour = "black", size = 1))

Más información

Estos análisis se han realizado utilizando el software R (v.4.1.0) y Rstudio (v. 1.4.1717)

Recuerda que todos nuestros códigos están almacenados en GitHub